Sliding Window Protocol Java Program
I am attempting to implement the following Basic Sliding Window algorithm in Java. I get the basic idea of it, but I am a bit confused by some the wording, specifically the sentence in bold:
C Programming Projects for $30 - $250. Part 1: Start-up First implement in C/C++ the Sliding Window Protocol PAR (unidirectional) as described in Fig 3.14 of your book Hi! I am professional C/C++/C#/Java programmer. I can do this project with highest quality! Best Regards, Szymszteinsl. A popular programming and development blog. Here you can learn C, C++, Java, Python, Android Development, PHP, SQL, JavaScript,.Net, etc. Here you will get sliding window protocol program in C.
A sliding window of fixed width w is moved across the file, and at every position k in the file, the fingerprint of its content is computed. Let k be a chunk boundary (i.e., Fk mod n = 0). Instead of taking the hash of the entire chunk, we choose the numerically smallest fingerprint of a sliding window within this chunk. Then we compute a hash of this randomly chosen window within the chunk. Intuitively, this approach would permit small edits within the chunks to have less impact on the similarity computation. This method produces a variable length document signature, where the number of fingerprints in the signature is proportional to the document length.
Please see my code/results below. Am I understanding the basic idea of the algorithm? As per the text in bold, what does it mean to 'choose the numerically smallest fingerprint of a sliding window within its chunk'? I am currently just hashing the entire chunk.
code:
results:
3 Answers
The simple answer is NO per my understanding (I once studied sliding window algorithm years ago, so I just remember the principles, while cannot remember some details. Metal slug anthology ppsspp cheat list. Correct me if you have more insightful understanding).
As the name of the algorithm 'Sliding Window', your window should be sliding not jumping as it says
in your quotes. That is to say the window slides one character each time.
Per my knowledge, the concept of chunks and windows should be distinguished. So should be fingerprint and hash, although they could be the same. Given it too expense to compute hash as fingerprint, I think Rabin fingerprint is a more proper choice. The chunk is a large block of text in the document and a window highlight a small portion in a chunk.IIRC, the sliding windows algorithm works like this:
- The text file is chunked at first;
- For each chunk, you slide the window (a 15-char block in your running case) and compute their fingerprint for each window of text;
- You now have the fingerprint of the chunk, whose length is proportional to the length of chunk.
The next is how you use the fingerprint to compute the similarity between different documents, which is out of my knowledge. Could you please give us the pointer to the article you referred in the OP. As an exchange, I recommend you this paper, which introduce a variance of sliding window algorithm to compute document similarity.
Another application you can refer to is rsync, which is a data synchronisation tool with block-level (corresponding to your chunk) deduplication. See this short article for how it works.
That is not a sliding window. All you have done is break up the input into disjoint chunks. An example of a sliding window would be
this program may help you. and please try to make more efficent
Not the answer you're looking for? Browse other questions tagged javaalgorithm or ask your own question.
This technique shows how a nested for loop in few problems can be converted to single for loop and hence reducing the time complexity.
Let’s start with a problem for illustration where we can apply this technique –
So, let’s analyze the problem with Brute Force Approach. We start with first index and sum till k-th element. We do it for all possible consecutive blocks or groups of k elements. This method requires nested for loop, the outer for loop starts with the starting element of the block of k elements and the inner or the nested loop will add up till the k-th element.
Consider the below implementation :
C++
// a subarray of size k usingnamespacestd; // Returns maximum sum in a subarray of size k. { intmax_sum = INT_MIN; // Consider all blocks starting with i. intcurrent_sum = 0; current_sum = current_sum + arr[i + j]; // Update result if required. } returnmax_sum; intmain() intarr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 }; intn = sizeof(arr) / sizeof(arr[0]); return0; |
Java
// O(n*k) solution for finding // of size k // Returns maximum sum in staticintmaxSum(intarr[], intn, intk) // Initialize result for(inti = 0; i < n - k + 1; i++) { for(intj = 0; j < k; j++) max_sum = Math.max(current_sum, max_sum); } // Driver code { intk = 4; System.out.println(maxSum(arr, n, k)); } // This code is contributed |
Python3
# maximum sum of a subarray of size k INT_MIN =-sys.maxsize -1# Returns maximum sum in a defmaxSum(arr, n, k): # Initialize result # starting with i. current_sum =0; current_sum =current_sum +arr[i +j]; # Update result if required. arr =[1, 4, 2, 10, 2, k =4; print(maxSum(arr, n, k)); # This code is contributed by mits |
C#
// finding maximum sum of a subarray usingSystem; classGFG { // Returns maximum sum in a staticintmaxSum(int[] arr, intn, { intmax_sum = int.MinValue; // Consider all blocks starting for(inti = 0; i < n - k + 1; i++) { for(intj = 0; j < k; j++) + arr[i + j]; // Update result if required. max_sum); } // Driver code { 0, 20 }; intn = arr.Length; } |
PHP
// O(n*k) solution for finding maximum sum of functionmaxSum($arr, $n, $k) $max_sum= PHP_INT_MIN ; // Consider all blocks for( $i= 0; $i< $n- $k+ 1; $i++) $current_sum= 0; $current_sum= $current_sum+ $max_sum= max($current_sum, $max_sum); } // Driver code $k= 4; echomaxSum($arr, $n, $k); // This code is contributed by anuj_67. |
Output :
It can be observed from the above code that the time complexity is O(k*n) as it contains two nested loops.
Window Sliding Technique
The technique can be best understood with the window pane in bus, consider a window of length n and the pane which is fixed in it of length k. Consider, initially the pane is at extreme left i.e., at 0 units from the left. Now, co-relate the window with array arr[] of size n and plane with current_sum of size k elements. Now, if we apply force on the window such that it moves a unit distance ahead. The pane will cover next k consecutive elements.
Consider an array arr[] = {5, 2, -1, 0, 3} and value of k = 3 and n = 5
Applying sliding window technique :
- We compute the sum of first k elements out of n terms using a linear loop and store the sum in variable window_sum.
- Then we will graze linearly over the array till it reaches the end and simultaneously keep track of maximum sum.
- To get the current sum of block of k elements just subtract the first element from the previous block and add the last element of the current block .
The below representation will make it clear how the window slides over the array.
This is the initial phase where we have calculated the initial window sum starting from index 0 . At this stage the window sum is 6. Now, we set the maximum_sum as current_window i.e 6.
Now, we slide our window by a unit index. Therefore, now it discards 5 from the window and adds 0 to the window. Hence, we will get our new window sum by subtracting 5 and then adding 0 to it. So, our window sum now becomes 1. Now, we will compare this window sum with the maximum_sum. As it is smaller we wont the change the maximum_sum.
Similarly, now once again we slide our window by a unit index and obtain the new window sum to be 2. Again we check if this current window sum is greater than the maximum_sum till now. Once, again it is smaller so we don’t change the maximum_sum.
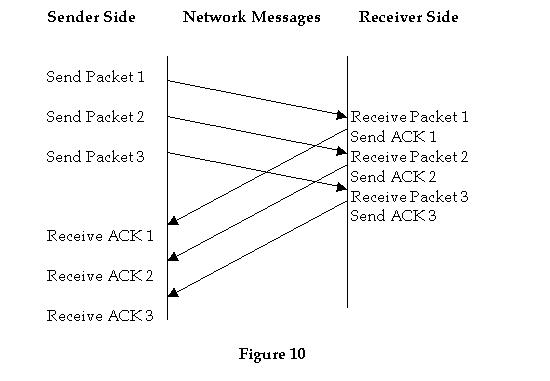
Go Back N Protocol
Therefore, for the above array our maximum_sum is 6.
code for the above description :
C++
Sliding Window Method
// a subarray of size k usingnamespacestd; // Returns maximum sum in a subarray of size k. { if(n < k) { return-1; intmax_sum = 0; max_sum += arr[i]; // Compute sums of remaining windows by // window and adding last element of intwindow_sum = max_sum; window_sum += arr[i] - arr[i - k]; } returnmax_sum; intmain() intarr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20 }; intn = sizeof(arr) / sizeof(arr[0]); return0; |
Java
// O(n) solution for finding // of size k // a subarray of size k. { if(n < k) { return-1; intmax_sum = 0; max_sum += arr[i]; // Compute sums of remaining windows by // window and adding last element of intwindow_sum = max_sum; window_sum += arr[i] - arr[i - k]; } returnmax_sum; publicstaticvoidmain(String[] args) intarr[] = { 1, 4, 2, 10, 2, 3, 1, 0, 20}; intn = arr.length; } // by prerna saini. |
Python3
# maximum sum of a subarray of size k INT_MIN =-sys.maxsize -1defmaxSum(arr, n, k): # n must be greater than k print('Invalid') max_sum =INT_MIN # removing first element of previous # current window. window_sum =window_sum -arr[i] +arr[i +k] arr =[1, 4, 2, 10, 2, 3, 1, 0, 20] n =len(arr) |
C#
// maximum sum of a subarray of size k // a subarray of size k. { // k must be greater Console.WriteLine('Invalid'); } // Compute sum of first window of size k for(inti = 0; i < k; i++) // removing first element of previous // current window. for(inti = k; i < n; i++) { max_sum = Math.Max(max_sum, window_sum); } // Driver code { intk = 4; Console.WriteLine(maxSum(arr, n, k)); } // This code is contributed by anuj_67. |
PHP
// O(n) solution for finding maximum sum of // subarray of size k. { if($n< $k) echo'Invalid'; } // Compute sum of first $max_sum= 0; $max_sum+= $arr[$i]; // Compute sums of remaining windows by // window and adding last element of $window_sum= $max_sum; { $max_sum= max($max_sum, $window_sum); } // Driver code $k= 4; echomaxSum($arr, $n, $k); // This code is contributed by anuj_67 |
Output :
Now, it is quite obvious that the Time Complexity is linear as we can see that only one loop runs in our code. Hence, our Time Complexity is O(n).
We can use this technique to find max/min k-subarray, XOR, product, sum, etc. Refer sliding window problems for such problems.
This article is contributed by Kanika Thakral. If you like GeeksforGeeks and would like to contribute, you can also write an article using contribute.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.
Recommended Posts:
Improved By : vt_m, AnnieAlford, Mithun Kumar, KyleMcClay